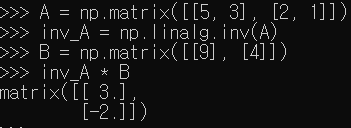
1. 벡터와 행렬의 관계
1) 점 P(3, 2)와 행렬A([2, 0],
[1, 2])를 곱하면 새로운 행렬 B가 나옴

① import numpy as np ← numpy 모듈을 np로 불러오겠음
② p = np.matrix([[3], [2]]) ← 2 x 1의 행렬이므로 점 P를 행렬(matrix)로 표시
A = np. matrix)[[2, 0], [1, 2]]) ← 행렬 A 입력
③ A * P ← 행렬의 곱
④ matrix([[6], [7]]) ← 새로운 행렬 B 나옴. 즉, 벡터의 끝 점이 바뀐 것
2. 도형의 대칭이동
1) x축에 대해 선대칭으로 변환
- x축에 대해 선 대칭은 x값의 부호는 그대로, y값의 부호는 반대가 됨
- 따라서 변환 행렬(단위 행렬)을 가지고 오고, y값이 부호가 반대이므로 A = ([1, 0],
[0, -1])을 곱해야 함
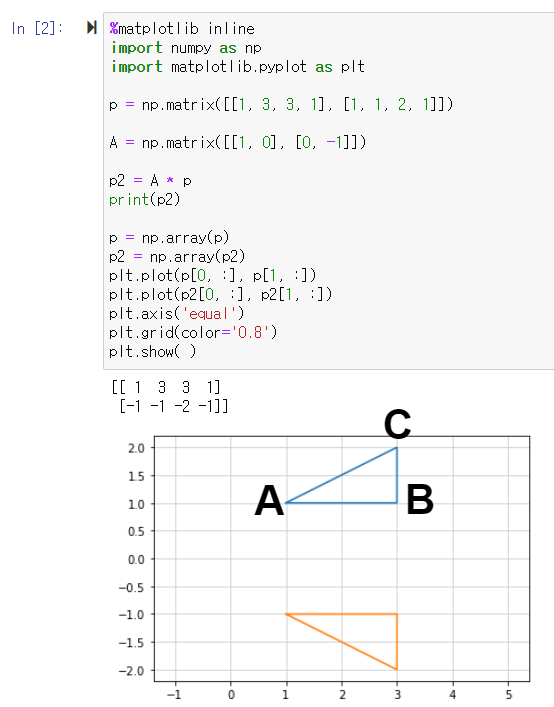
① %matplotlib inline
import numpy as np ← numpy 모듈을 np로 불러오겠음
import matplotlib.pyplot as plt ← pyplot을 plt로 불러오겠음
② p = np.matrix([[1, 3, 3, 1], [1, 1, 2, 1]]) ← <A → B → C → A> 순서로 그림을 그렸으므로 이 순서로 좌표 입력
A = np.matrix([[1, 0], [0, -1]]) ← x축 대칭인 변환행렬
③ p2 = A * p ← 변환한 행렬
print(p2) ← x축에 대해 대칭으로 변환된 행렬 p2를 보여라
④ p= np. array(p)
p2 = np.array(p2) ← p와 p2를 이차원 행렬로 배열하라
(원래 2 x 4 였음 따라서 우린 x와 y만 있는 2차원에 이것을 그릴것)
⑤ plt.plot(p[0, :], [p[1, :]) ← 배열 p의 첫 번째 행과 두 번째 행을 그려라
(즉 x좌표와 y좌표, 코딩에서 숫자는 항상 0부터 시작)
plt.plot(p2[0, :], p2[1, :]) ← 배열 p2의 첫 번째 행과 두 번째 행을 그려라
plt.axis('equal') ← x와 y축을 동등한 크기로 맞춰라
plt.grid(color='0.8') ← 간격을 0.8의 굵기로 그려라
plt.show( ) ← 보여줘라
2) y축에 대해 선대칭
- y축에 대해 선 대칭은 y값의 부호는 그대로, x값의 부호는 반대가 됨
- 따라서 변환 행렬(단위 행렬)을 가지고 오고, x값이 부호가 반대이므로 A = ([-1, 0],
[0, 1])을 곱해야 함

① (import numpy as np) ← numpy 모듈을 np로 불러오겠음
② p = np.matrix([[1, 3, 3], [1, 1, 2]]) ← 삼각형 ABC의 좌표 넣어 행렬 입력
A = np. matrix)[[-1, 0], [0, 1]]) ← y축에 선대칭인 변환행렬 입력
③ A * P ← 선대칭한 행렬
④ matrix([[-1, -3, -3], [1, 1, 2]])
3) 원점에 대해 선대칭

① (import numpy as np) ← numpy모듈을 np로 불러오겠음
② p = np.matrix([[1, 3, 3], [1, 1, 2]]) ← 삼각형 ABC의 좌표를 입력한 행렬 입력
A = np. matrix)[[-1, 0], [0, -1]]) ← 원점이므로 모든 부호가 바뀐 변환행렬 입력
③ A * P ← 원점에 대해 선대칭된 행렬을 구해라
④ matrix([[-1, -3, -3], [-1, -1, -2]])
4) 직선 y = x에 대해 선대칭
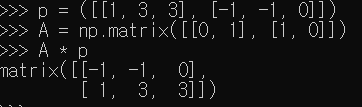
① (import numpy as np) ← numpy 모듈을 np로 불러와라
② p = np.matrix([[1, 3, 3], [-1, -1, 0]]) ← 삼각형 ABC의 좌표를 입력한 행렬을 입력해라
A = np. matrix)[[0, 1], [1, 0]]) ← y=x에 대한 선대칭으므로 둘의 위치가 바뀐 변환 행렬을 입력하라
③ A * P ← y = x에 대해 선대칭된 행렬을 구하라
④ matrix([[-1, -1, 0], [1, 3, 3]])
3. 도형을 확대하고 축소하기
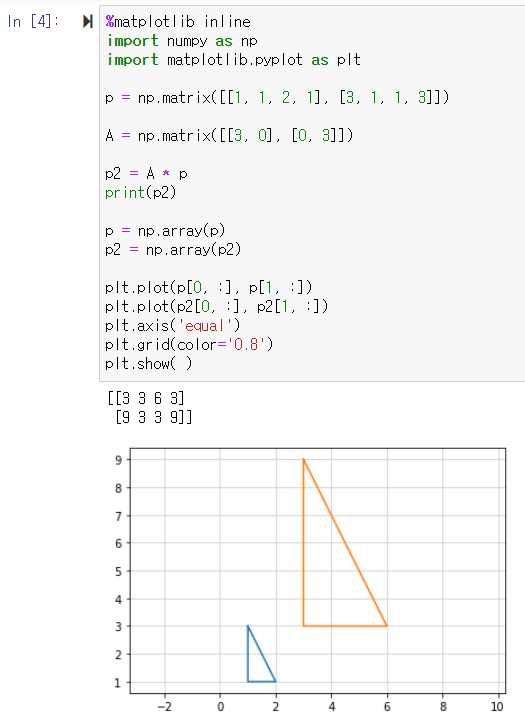
① %matplotlib inline
import numpy as np ← numpy 모듈을 np로 불러오겠음
import matplotlib.pyplot as plt ← pyplot을 plt로 불러오겠음
② p = np.matrix([[1, 1, 2, 1], [3, 1, 1, 3]]) ← 삼각형 ABC (그리는 순서대로 좌표 입력) 좌표를 입력한 행렬 입력
A = np.matrix([[3, 0], [0, 3]]) ← 3배를 확대시키고 싶은 것이므로 변환행렬에 실수배 3을 곱하면 됨.
③ p2 = A * p ← 3배 확대된 행렬 구해라
print(p2) ← 3배 확대된 행렬을 보여줘라
④ p= np. array(p) ← p의 배열을 이차원으로 나타내라
p2 = np.array(p2) ← p2의 배열을 이차원으로 나타내라
⑤ plt.plot(p[0, :], [p[1, :]) ← 배열 p의 첫 번째 행과 두 번째 행을 그려라 (x좌표, y좌표)
plt.plot(p2[0, :], p2[1, :]) ← 배열 p2의 첫 번째 행과 두 번째 행을 그려라
plt.axis('equal') ← x와 y의 크기는 균일하게 맞춰라
plt.grid(color='0.8') ← 0.8의 굵기로 격자무늬를 그려라
plt.show( ) ← 보여줘라
4. 도형을 회전시키기
1) 회전 행렬을 만드는 방법


① %matplotlib inline
import numpy as np ← numpy모듈을 np로 불러와라
import matplotlib.pyplot as plt ← pyplot을 plt로 가져와라
② p = np.matrix([[3, 3, 5, 5, 3], [3, 1, 1, 3, 3]]) ← 사각형 ABCD의 좌표를 행렬로 입력해라
③ th = np.radians(45) ← 반 시계방향으로 45도 회전해라 (도수법을 호도법으로 전환)
A = np.matrix([[np.cos(th), np.sin(-th)], [np.sin(th), np.cos(th)]]) ← 위의 회전행렬을 입력
④ p2 = A * p ← 반 시계방향으로 45도 회전한 행렬 구하기
print(p2) ← 반 시계방향으로 45도 회전한 행렬을 나타내라
⑤ p = np.array(p) ← p를 이차원 배열로 나타내라
p2 = np.array(p2) ← p2를 이차원 배열로 나타내라
plt.plot(p[0, :], [p[1, :]) ← 배열 p의 첫번째, 두번째 행을 그려라
plt.plot(p2[0, :], p2[1, :]) ← 배열 p2의 첫번째, 두번째 행을 그려라
plt.axis('equal') ← x축과 y축을 균일하게 맞춰라
plt.grid(color='0.8') ← 0.8의 굵기로 격자 무늬를 넣어라
plt.show( ) ← 보여줘라
5. 2 X 2 행렬이 아닌 3 X 3 행렬 사용하기
1) 대칭 이동이나 확대 및 축소할 땐 변환 행렬을 2x2 행렬을 사용했지만 평행 이동시 3x3의 행렬을 이용해야 함
(평행 이동은 덧셈이기 때문)
2) 그렇기 때문에 동차 좌표 방식을 도입
- 일반적인 이차원 좌표 (x, y)에 매개변수 w 도입하여 (wx, wy, w)라고 표현
- 매개변수 w 값은 항상 1이므로 x와 y값은 변화하지 않음
3) 삼각형 ABC를 x축 방향으로 2만큼 평행이동, y축 방향으로 3만큼 평행이동 하는 방법
- 동차좌표로 표현하면 → ([1, 0, 2],
[0, 1, 3],
[0, 0, 1])
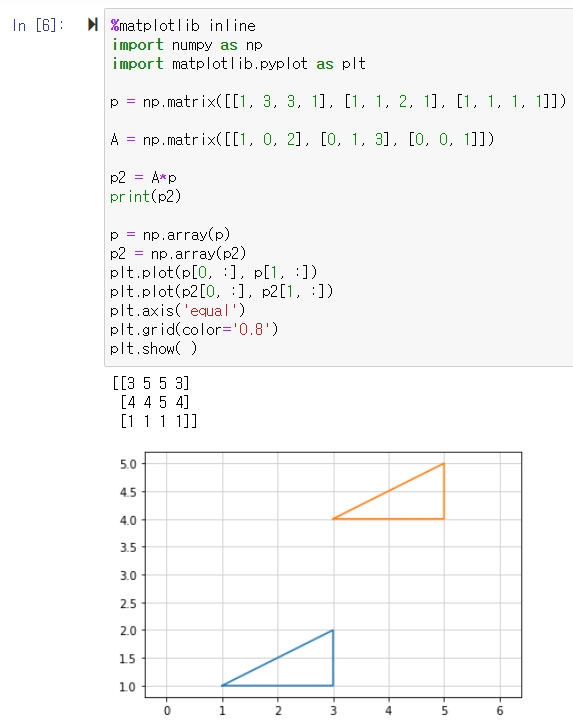
① %matplotlib inline
import numpy as np → numpy모듈을 np로 불러오겠음
import matplotlib.pyplot as plt → pyplot을 plt로 불러오겠음
② p = np.matrix([[1, 3, 3, 1], [1, 1, 2, 1], [1, 1, 1, 1]]) ← 삼각형 ABC (그리는 순서대로) 행렬 입력
A = np.matrix([[1, 0, 2], [0, 1, 3], [0, 0, 1]]) ← 동차좌표를 이용해 평행이동을 하는 변환 행렬 입력
③ p2 = A * p ← 변환된 행렬 구하기
print(p2) ← 변환된 행렬 나타내라
④ p = np.array(p) ← 행렬 p를 이차원 배열로 나타내라
p2 = np.array(p2) ← 행렬 p2를 이차원 배열로 나타내라
plt.plot(p[0, :], [p[1, :]) ← 배열 p의 첫번째, 두번째 행을 그려라
plt.plot(p2[0, :], p2[1, :]) ← 배열 p2의 첫번째, 두번째 행을 그려라
plt.axis('equal') ← x축과 y축의 크기를 균일하게 맞추어라
plt.grid(color='0.8') ← 격자무늬를 0.8의 굵기로 그려라
plt.show( ) ←보여줘라
6. 일차변환의 조합
1) 삼각형 ABC를 x축 방향으로 2만큼, y축 방향으로 3만큼 평행이동한 후에 반 시계 방향으로 90도 회전시키기
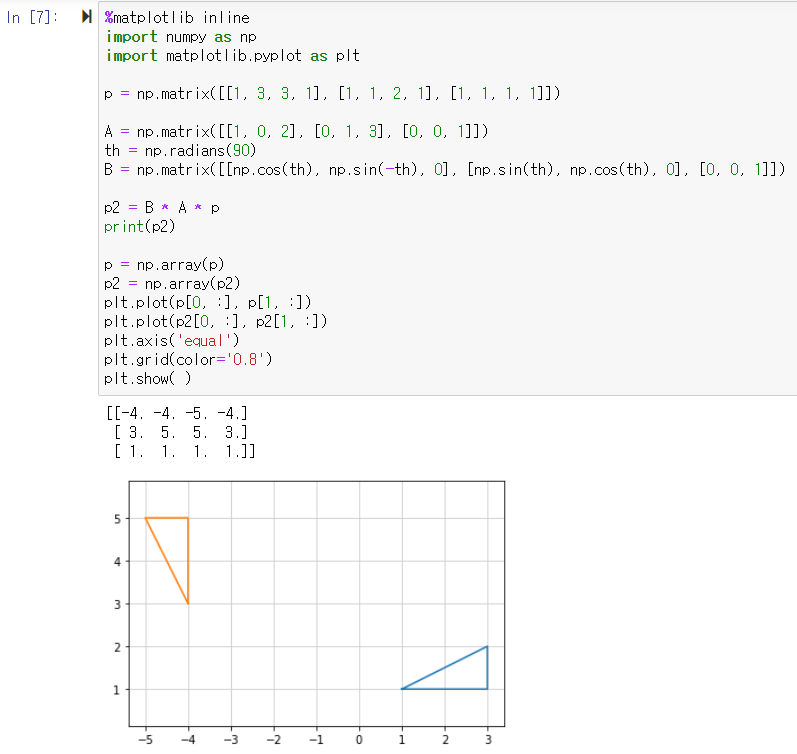
① %matplotlib inline
import numpy as np ← numpy 모듈을 np로 불러와라
import matplotlib.pyplot as plt ← pyplot을 plt로 불러와라
② p = np.matrix([[1, 3, 3, 1], [1, 1, 2, 1], [1, 1, 1, 1]]) ← 삼각형ABC의 좌표를 행렬로 입력하라
③ A = np.matrix([[1, 0, 2], [0, 1, 3], [0, 0, 1]]) ← 동차좌표에서 평행이동하여 행렬을 입력해라
th = np.radians(90) ← 도수법을 호도법으로 전환함
A = np.matrix([[np.cos(th), np.sin(-th), 0], [np.sin(th), np.cos(th), 0], [0, 0, 1]]) A
← 동차좌표가 원래 ([1, 0, 0], [0, 1, 0], [0, 0, 1]) 이었으므로 동차좌표를 이용해 회전 행렬 입력
④ p2 = B * A * p ← 평행이동하고, 회전까지 한 행렬 구하기
print(p2) ← 평행이동하고 회전한 행렬을 나타내라
⑤ p = np.array(p) ← 행렬 p를 이차원 배열로 나타내라
p2 = np.array(p2) ← 행렬 p2를 이차원 배열로 나타내라
plt.plot(p[0, :], [p[1, :]) ← 배열 p의 첫번째, 두번째 행을 그려라
plt.plot(p2[0, :], p2[1, :]) ← 배열 p2의 첫번째, 두번째 행을 그려라
plt.axis('equal') ← x축과 y축의 크기를 균일하게 해라
plt.grid(color='0.8') ← 0.8의 굵기로 격자무늬를 그려라
plt.show( ) ← 보여줘라
'파이썬으로 다시 배우는 핵심고등수학 (python) > 05장 : 행렬' 카테고리의 다른 글
| 5-2. 행렬의 연산 (0) | 2021.02.05 |
|---|